
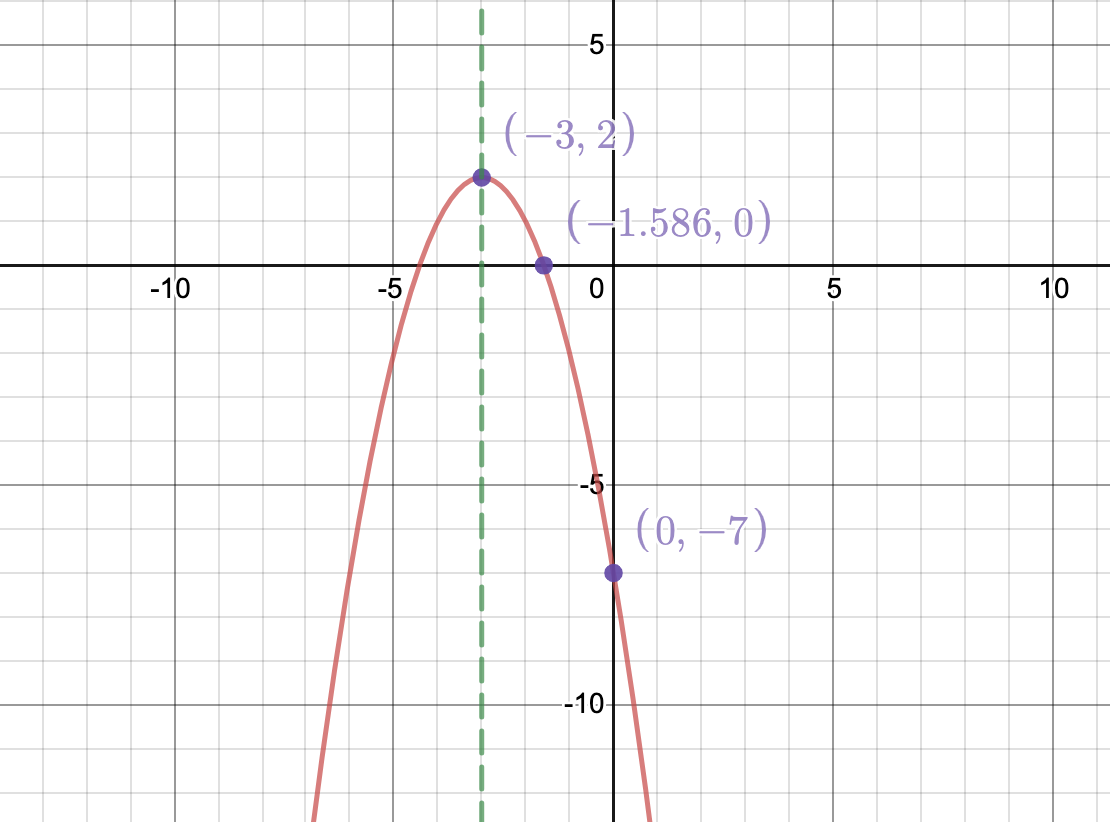
These are the points the graph crosses the 𝑥 - a x i s at. Graphs of quadratics can have 0, 1, or 2 𝑥-intercepts.All graphs of quadratics have a 𝑦-intercept at the point ( 0, 𝑐 ) this is the point where the graph.Then the graph of the quadratic will open downward. If 𝑎 > 0, then the graph of the quadratic will open upward if 𝑎 < 0, All quadratic curves have a parabolic shape.Quadratic functions have the form 𝑓 ( 𝑥 ) = 𝑎 𝑥 + 𝑏 𝑥 + 𝑐 , for some constants 𝑎, 𝑏, and 𝑐,.Properties: Quadratic Functions and Their Graphs
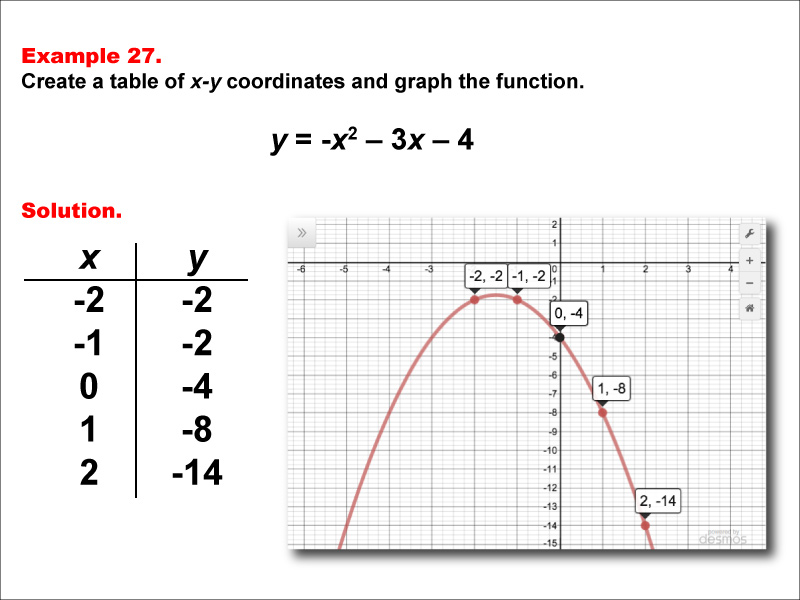
In our first example, we will determine the 𝑥-intercepts of a quadratic curve from its graph. We could say that the 𝑦-intercept of the second graph is at 9. For example, we could say that the 𝑥-intercepts of the second graph are at − 3 and 3. It is worth noting that since the 𝑦-coordinates of the 𝑥-intercepts are 0, we often only talk about the 𝑥-coordinates The 𝑥-coordinates of these points tell us the input values at which the function outputs 0. We can see that the first curve has no 𝑥-intercepts and the second has two at the points ( − 3, 0 )Īnd ( 3, 0 ). Second, the 𝑥-intercepts of the graph will be the points on the graph where 𝑦 = 0, which is where the curve crosses It is worth noting that we can find the 𝑦-intercept of the graph of the function In the first graph, this is ( 0, 4 ), and in the second, this is ( 0, 9 ). There are also many useful points we can label to help us determine and convey information about the graph.įirst, we recall that the 𝑦-intercept of the graph will be the point on the graph where 𝑥 = 0, which is where the curve crosses the We can see this in the two given graphs the first graph has a positive leading coefficient and its graph opens upward, while the second hasĪ negative leading coefficient and its graph opens downward. If 𝑎 > 0, then the parabola opens upward, and if 𝑎 < 0, then the parabola Tells us if the parabola opens upward or downward. In fact, all quadratics have this shape, and the sign of the constant 𝑎 We note that these graphs have a very similar shape, known as a parabola. For example, let’s consider the graphs of the two quadratic equations We can better understand quadratics by considering their graphs. A quadratic equation is an equation in the form 𝑦 = 𝑓 ( 𝑥 ), where 𝑓 ( 𝑥 ) Quadratic functions have the form 𝑓 ( 𝑥 ) = 𝑎 𝑥 + 𝑏 𝑥 + 𝑐 , for some constants 𝑎, 𝑏, and 𝑐, To do this, let’s start by recalling what we mean by a quadratic function: it is a single-variable degree-two polynomial function. In particular, we can use the graphs of quadratic functions to easily determine information about the maximum and minimum values and when the outputs will be equal to zero. This means we can use quadratic equations to analyze these scenarios. Identify the minimum and maximum values of many different variables such as speed, cost, and area. Businesses can use them to forecast revenues and design packaging to minimize waste.
They can determine the paths of moving objects, from bouncing balls to Quadratic equations are used in everyday life, in science, business, and engineering.
#Quadratic function graph how to#
Given a quadratic equation, the student will use graphical methods to solve the equation.In this explainer, we will learn how to graph any quadratic function using a table of values and a given interval and identify the features of the graph. The student is expected to:Ī(8)(A) solve quadratic equations having real solutions by factoring, taking square roots, completing the square, and applying the quadratic formula

The student formulates statistical relationships and evaluates their reasonableness based on real-world data. The student applies the mathematical process standards to solve, with and without technology, quadratic equations and evaluate the reasonableness of their solutions. The student is expected to:Ī(1)(C) select tools, including real objects, manipulatives, paper and pencil, and technology as appropriate, and techniques, including mental math, estimation, and number sense as appropriate, to solve problemsĪ(1)(D) communicate mathematical ideas, reasoning, and their implications using multiple representations, including symbols, diagrams, graphs, and language as appropriateĪ(8) Quadratic functions and equations. The student uses mathematical processes to acquire and demonstrate mathematical understanding. Let's explore how to solve quadratic equations by looking at their graphs.Ī(1) Mathematical process standards.


 0 kommentar(er)
0 kommentar(er)
